What is Depth-First Search (DFS)?

Definition

Depth-First Search, or DFS, is a graph traversal algorithm that starts at a root node and visits every node in the graph. It get’s the name depth-first search because the algorithm traverses down a collection of edge-connected nodes rather than traversing across those nodes.

Depth-First Search can be applied to any type of graph, including trees, graphs with circuits, and disconnected graphs. For our usage, we will be applying it to a tree (a connected graph with no circuits), but the algorithm works similarly for all types of graphs.

Explaination of the algorithm

Depth-First Search always starts at the root node of a graph. For trees, this can be the node at the top at the \(0^{\text{th}}\) level, but can just be an arbitrary node other graphs. Depending on the type of DFS used, search can begin elsewhere in trees. During the traversal process, DFS makes use of two collection data structures: one to store the nodes that have just been visited, and one to store the nodes adjacent to those nodes that will be visited next. When a node is visited, it is marked as such by adding it to the visited collection, and all nodes adjacent to that node are added to the stack collection. The algorithm finishes once every node has been visited.

Here is a visualization of a DFS algorithm running on a graph with the root node as 2:

DFS Example
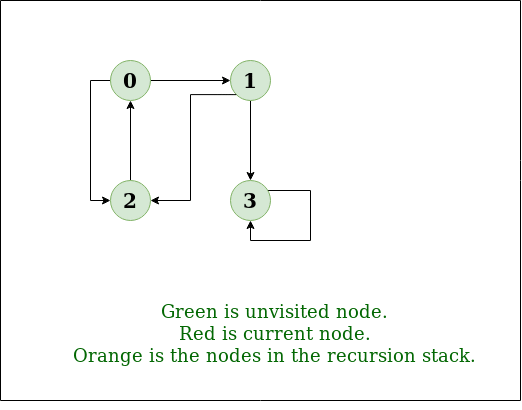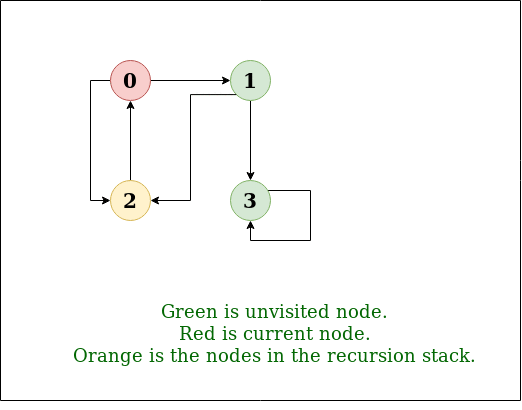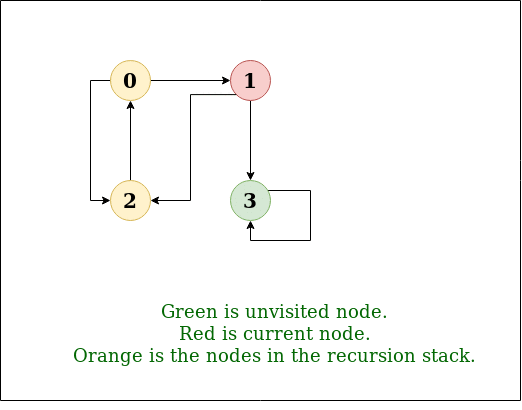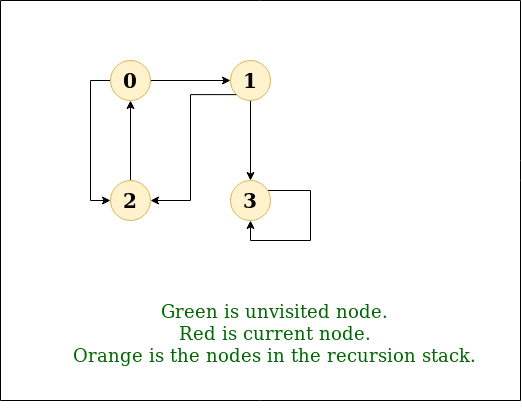
Image Source: GeeksForGeeks

Depth-First Search Step-by-Step

Let’s go through a pass of a DFS algorithm step by step.

  1. Intially, every graph node is unvisited, and no nodes are up next to be visited. DFS Step 1
    Image Source: GeeksForGeeks

  2. The root 0 node is chosen and added to visited . It’s adjacent nodes, 1, 2, and 3, are added to the stack. DFS Step 2
    Image Source: GeeksForGeeks

  3. The algorithm traverses the graph in the order of the nodes in the stack. 1 is first, so it is popped off the stack and the algorithm traverses to 1. 1 is added to visited. It has no adjacent nodes, so the stack stays the same. DFS Step 3
    Image Source: GeeksForGeeks

  4. 2 is the next node on the stack, so it is popped off and the algorithm traverses to 2. 2 is added to visited, and it’s adjacent nodes, 3 and 4, are added to the stack. DFS Step 4
    Image Source: GeeksForGeeks

  5. 4 is the next node on the stack, so it is popped off and the algorithm traverses to 4. 4 is added to visited. It has no adjacent nodes, so the stack stays the same. DFS Step 5
    Image Source: GeeksForGeeks

  6. 3 is the last node on the stack, so it is popped off and the algorithm traverses to 3. 3 is added to visited. It has no adjacent nodes, so the stack stays the same. DFS Step 6
    Image Source: GeeksForGeeks

At this point, the stack is empty and all nodes have been visited, so the search ends.

Applying DFS to a tree

We’ve seen how Depth-First Search works on a graph with circuits, but how does it work on a tree? DFS works very similar for trees, but can be implemented in a variety of ways depending on what you plan to do with the tree. For our implementation, I believe the most useful traversal method will be Pre-order NLR search. This method uses the tree’s root as the root node for DFS. Pre-order refers to when the tree nodes are marked as visited - before recursing down the tree. NLR represents the direction the nodes will be searched - from left to right. In Pre-order NLR Depth-First Search, nodes are marked as visited, the left side of the tree is traversed fully, then the right side is traversed fully.

The GIF below models Pre-order NLR DFS. Once the full length of the tree is traversed on the left hand side, the algorithm goes back up to the next parent node to traverse the parent’s right hand side. After the algorithm traverses node 4, it returns back up to node 1 and traverses down the left hand side of node 5. The algorithm then returns to node 5 and traverses the right side down to node 8. From there, the algorithm returns to node 1 and traverses down the right hand size of the root node to node 10.

DFS Tree Example
Image Source: Wikipedia

How can this be used to search for nodes?

Depth-First Search can be a very useful algorithm for accessing data in an entire tree, but it can be also used to locate a specific node within a tree. This is often done by prematurely ending the search when a node is visited that meets a specific criteria or choosing to only search a portion of the tree. DFS alone isn’t useful for searches in and of itself, but when woven into a specific context and used in a limited way within that context, it can be a very powerful tool to efficiently find data within a tree or graph.

Complexity Analysis

Depth-First Search takes \(O(V + E)\) time, where \(V\) is the number of vertices in the graph and \(E\) is the number of edges in the tree. In general, this algorithm takes \(O(n)\), or linear time.

The space complexity of the algorithm depends on the maximum recursion depth used in the imlementation. A default implementation that traverses every node will reach a maximum recursion depth of \(V\). At minimum, the algorithm stores a stack with a variable number of nodes to visit at any given time, and it also stores an array of all the visited nodes. Because of this, the algorithm uses \(O(V)\), or linear space to store nodes.

Just for fun…an XKCD comic about tree searches

Because computer scientists are definitely funny too

XKCD Comic
Image Source: XKCD